Natuurkundige principes voor de audicien
InleidingNatuurkunde is overal om ons heen aanwezig. Soms wat duidelijker, soms wat minder duidelijk. De principes van de natuurkunde worden bij het aanpassen van hoortoestellen en alles wat er omheen hoort, vaak onbewust in ons voordeel gebruikt. Maar soms moet er wel degelijk rekening gehouden worden met het feit dat een bepaalde handeling een (negatief) effect heeft.
Er zal in de audicienpraktijk zeker niet dagelijks gerekend worden met moeilijke natuurkundige formules. Maar het is goed om op de hoogte te zijn van de verschillende natuurkundige principes waar de audicien mee te maken krijgt.
Geluid
De luidheid van geluid
De eenheid van geluidsniveau is de decibel (dB). Maar de decibel is niet een eenheid die rechtstreeks gemeten kan worden. Dat lijkt wel zo, omdat er verschillende meetinstrumenten zijn die meteen het geluidsniveau in decibel weergeven. Maar deze meetinstrumenten gebruiken een formule om de gemeten geluidsdruk of de gemeten geluidsintensiteit snel om te rekenen naar decibel.
Geluid ontstaat doordat lucht in trilling wordt gebracht, bijvoorbeeld door de conus van een luidspreker. De heengaande beweging van de conus van een luidspreker duwt eerst de luchtmoleculen een klein beetje in elkaar. De teruggaande beweging trekt de luchtmoleculen weer een beetje uit elkaar. Daardoor ontstaan er lokaal luchtdrukverschillen, die geleidelijk in elkaar overgaan van een maximum naar een minimum. Deze drukverschillen worden waargenomen als geluid. Met andere woorden, geluid is een variatie in luchtdruk. Deze luchtdrukvariatie kan gemeten worden in de eenheid van druk: Pascal (Pa).Hoe luider een geluid is, des te groter is de geluidsdruk.
Het in beweging brengen van de luchtmoleculen kost energie. Dus geluid is ook te beschouwen als een vorm van energie. Deze energie kan worden gemeten en weergegeven in de eenheid van energie: W/m2, Watt per vierkante meter. Hoe harder een geluid is, des te meer energie kost het om dit geluid te produceren.
De weergave van de luidheid van een bepaald geluid in geluidsdruk of in geluidsintensiteistniveau is echter wat onpraktisch.Zo kan van de luidheid van spraak op conversatieniveau gezegd worden dat het een geluidsdruk heeft van 0,02 Pa of een geluidsintensiteit van 1.10-6 W/m 2.
Dat is wat onwennig, maar het is niet onmogelijk. Het probleem is meer het bereik van het oor. Het oor heeft een behoorlijk bereik in de luidheid van geluiden die gehoord kunnen worden. In tabel 1 worden deze grenzen weergegeven.
| Geluidsdruk (Pa) | Geluidsintensiteit (W/m2) | |
|---|---|---|
| Hoordrempel | 2.10-5 | 1.10-12 |
| Pijngrens | 20 | 1 |
| Verschil min-max | factor 1 miljoen | factor 1 biljoen |
Er is dus een groot verschil tussen het minimum en het maximum van het gehoor. Dat is wat onpraktisch. Daarom is er een andere eenheid voor geluid ingevoerd, de decibel. Door van de gemeten waarden van geluidsdruk of geluidsintensiteit de logaritme te nemen, kunnen de grote verschillen binnen een kleiner gebied worden weergegeven. De formules die daarvoor gebrukt worden zijn:
Omdat in het dagelijks gebruik de referentiewaarde altijd dezelfde waarde heeft,
zou deze formule dus ook geschreven kunnen worden als:
Lp = 20.log(P/2.10-5)
zou deze formule dus ook geschreven kunnen worden als:
Lp = 20.log(P/2.10-5)
- Voor geluidsdruk:
Lp = 20.log(P/P0)
Formule 1: Berekening van het geluidsdrukniveau vanuit de gemeten geluidsdruk.
In deze formule is "P" de gemeten geluidsdruk. Voor "P0" wordt als referentiewaarde de geluidsdruk van de hoordrempel genomen: 2.10-5 Pa. - Voor geluidsintensiteit:
LI = 10.log(I/I0)
Formule 2: Berekening van het geluidsintensiteisiveau vanuit de gemeten geluidsintensiteit.
In deze formule is "I" de gemeten geluidsintensiteit. Voor "I0" wordt als referentiewaarde de geluidsintensiteit van de hoordrempel genomen: 10-12 W/m2.
Omdat in het dagelijks gebruik de referentiewaarde altijd dezelfde waarde heeft,
zou deze formule dus ook geschreven kunnen worden als:
Lp = 10.log(I/10-12)
Door deze berekening wordt nu niet meer de geluidsdruk (in Pa) of de geluidsintensiteit (in W/m2) weergegeven, maar het
geluidsdrukniveau en het geluidsintensiteisniveau, beiden uitgedrukt in decibel. Tegelijkertijd wordt hiermee de gemeten luidheid gerelateerd aan de
hoordrempel van de goedhorende mens. De decibel is dus een relatieve eenheid die als het ware aangeeft hoeveel luider een bepaald geluid is ten opzichte van
de hoordrempel. Als met bovenstaande formules het bereik van het gehoor wordt berekend, dan levert dat het volgende op:zou deze formule dus ook geschreven kunnen worden als:
Lp = 10.log(I/10-12)
De geluidsdruk bij de hoordrempel bedraagt 2.10-5 Pa. Ingevuld in de formule wordt dat:
Lp = 20.log (2.10-5/ 2.10-5) Dit wordt: Lp = 20.log 1
Verder uitgewerkt:
Lp = 20.log 1 De logaritme van 1 nemen (rekenmachine): log 1 = 0
Invullen in de formule:
Lp = 20 x 0
Dus het antwoord wordt:
Lp = 0 dB
Het geluidsdrukniveau bij de hoordrempel is gelijk aan 0 dB. De omrekening van de andere waarden naar decibel gaan op soortgelijke wijze. Om het geheel niet te verwarrend te maken, worden de berekening van het geluidsdrukniveau bij de pijngrens en de berekening van het geluidsintensiteitsniveau bij zowel de hoordrempel als bij de pijngrens in een apart scherm weergegeven. Dat kan worden geopend door op het ikoontje hiernaast te klikken.
Het gebruik van deze berekeningen met omzetting naar de eenheid decibel heeft als resultaat dat er een veel overzichtelijker en meer aansprekend bereik van het gehoor ontstaat. Het bereik van het gehoor loopt nu, voor het geluidsdrukniveau en het geluidsintensiteitsniveau van 0 dB (hoordrempel) tot 120 dB (pijngrens).
Maar let op: geluid kan ook zachter zijn dan 0 dB, net zoals het ook harder kan zijn dan 120 dB. Deze waarden geven alleen de grenzen aan van het gehoor.
De hier berekende decibel is de dB SPL, decibel Sound Pressure Level.
De frequentie van geluid
Naast luidheid heeft geluid ook een toonhoogte. De toonhoogte die wordt waargenomen wordt bepaald door de frequentie waarmee de conus van de luidspreker heen en weer gaat. Hoe vaker de conus per seconde op en neer gaat, des te hoger is de frequentie die wordt waargenomen. De frequentie van een toon wordt uitgedrukt in de eenheid Hertz (Hz). Geluid is, zoals hierboven wordt weergegeven, een afwisseling van luchtdrukverhogingen en luchtdrukverlagingen. Bij een bepaalde frequentie hoort een even groot aantal luchtdrukverhogingen en verlagingen. In figuur 1 wordt dit grafisch weergegeven.
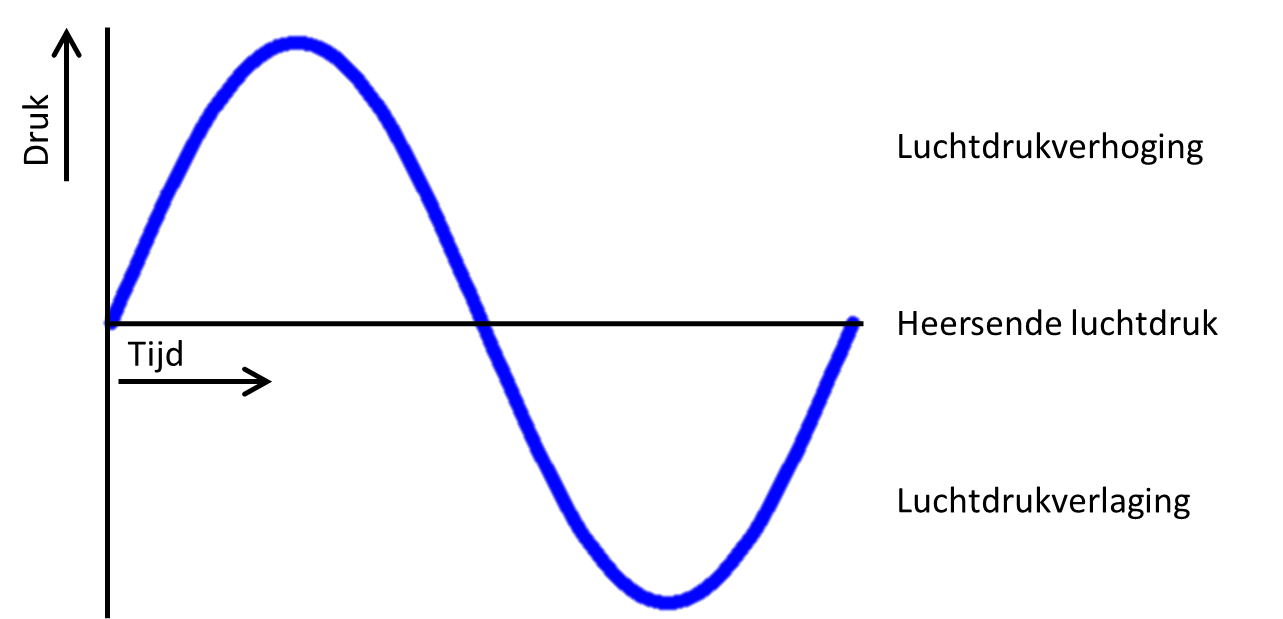
Figuur 1: Geluid is een afwisseling van drukverhogingen en drukverlagingen
De grafische weergave van deze drukwisselingen heeft bij een zuivere toon de vorm van een sinus. Geluid wordt daarom ook wel een sinusvormig signaal genoemd. Een zuivere toon is een toon die maar uit één frequentie bestaat, bijvoorbeeld 1000 Hz. In de praktijk komt dit nauwelijks voor. De noot A in de muziek heeft een frequentie van 440 Hz. Als deze noot gespeeld wordt met een bepaald muziekinstrument heeft niet alleen die ene frequentie van 440 Hz in zich, maar ook een aantal hogere en lagere frequenties. Door deze extra frequenties kunnen verschillende muziekinstrumenten worden herkend.
In figuur 1 is op de verticale as de (geluids)druk weergegeven. Het midden is daarbij de heersende luchtdruk. Met andere woorden, geluid is een variatie in de heersende luchtdruk. De heersende luchtdruk is ruwweg gelijk aan 100.000 Pa. Hierboven is aangegeven dat de geluidsdruk bij de pijngrens gelijk is aan 20 Pa. De drukwisseling bij de bovengrens van wat het oor kan verdragen is dus nog maar 20/100.000 ofwel 0,02% van de normale luchtdruk. Dit geeft goed aan wat de gevoeligheid van het oor is. Hiermee is ook meteen aangegeven dat de hoogte van de sinus een maat is voor de luidheid van een toon.
Op de horizontale as van figuur 1 wordt de tijd weergegeven. Hiermee kan worden aangeduid hoe lang het duurt voordat er een hele cyclus van drukverhoging en drukverlaging is verstreken. Een hele cyclus wordt ook wel een periode genoemd. De tijd die nodig is voor een hele periode, wordt periodetijd genoemd. Dit is van belang, want ook de frequentie van een toon kan niet direct worden gemeten. Er kan wel gemeten worden hoe lang een periode duurt. Deze periodetijd wordt dan snel omgerekend naar frequentie. De formule daarvoor is (formule 3):
f = 1/T
Formule 3: Berekening van de frequentie uit de gemeten periodetijd.
In deze formule is "T" de gemeten periodetijd (in seconden). Voor de berekende frequentie wordt de "f" (in Hz) gebruikt.
Uit formule 3 is ook af te leiden dat bij een kortere periodetijd de frequentie hoger wordt. En andersom, als de frequentie lager wordt, wordt de periodetijd langer. Het menselijk oor heeft ook bij het horen van frequenties bepaalde grenzen. Algemeen wordt aangenomen dat het frquentiebereik van een goedhorende ligt lussen 20 Hz en 20.000 Hz. Deze bovengrens is echter zeer afhankelijk van de leeftijd. Met het ouder worden neemt de gevoeligheid van het gehoor voor de hogere frequenties af.
De golflengte van geluid
Geluid verspreidt zich in een medium met een bepaalde snelheid. De geluidssnelheid in lucht bedraagt 343 m/s. Dat kan gebruikt worden als een vast gegeven. In werkelijkheid varieert de snelheid van het geluid onder anderen met de hoogte van de luchtdruk en de temperatuur. Deze schommelingen zijn echter niet heel groot en worden daarom bijna nooit meegenomen in berekeningen. Hier wordt als de snelheid van het geluid in lucht 343 m/s gebruikt.
Als de voortplantingssnelheid van geluid 343 m/s bedraagt, dan heeft dat bepaalde gevolgen. Het volgende voorbeeld kan mogelijk een en ander verduidelijken.
Uit een luidspreker, opgesteld in het vrije veld, komt een toon van 100 Hz. Deze toon van 100 Hz heeft als gevolg dat er in één seconde 100 drukwisselingen ofwel 100 periodes (sinussen) optreden.
In diezelfde seconde legt het geluid 343 meter af.
Er bevinden zich in deze 343 meter dus 100 sinussen. Dat houdt in dat elke sinus een lengte heeft van 343 / 100 = 3,43 meter. Ofwel: een toon van 100 Hz heeft een golflengte van 3,43 meter.
Er is een vaste relatie tussen de snelheid, de frequentie en de golflengte van het geluid. Deze relatie wordt weergegeven in formule 4
λ= v/f
Formule 4: Berekening van de golflengte bij een bepaalde frequentie
In deze formule is "λ" (de Griekse letter lambda) het symbool dat gebruikt wordt voor de golflengte met als eenheid de meter (m). De "f" staat weer voor de frequentie (Hz). De "v" is het gebruikte symbool voor de snelheid, in dit geval de geluidssnelheid (343 m/s).
De golflengte van een hoge frequentie is klein, zoals berekend kan worden. De golflengte van een lagere frequentie is groter.
Er is dus een relatie tussen frequentie en golflengte. Hoewel het soms zo lijkt, is er geen relatie tussen luidheid (amplitude) en frequentie. Door op het ikoontje hiernaast te klikken opent een scherm waarbij het mogelijk is om zowel de frequentie als de luidheid te veranderen. Dan is te zien dat beiden apart van elkaar veranderen.
Golfverschijnsel
Geluid wordt ook wel een "golfverschijnsel" genoemd. Dit is omdat de veranderingen in druk elkaar opvolgen als in een sinusgolf. (figuur 1). Als geluid zich in het vrije veld voortbeweegt, dan wordt dit geluid beschreven als een "lopende golf". Vanuit de bron beweegt het geluid zich alle kanten op, zolang het geen obstakels tegen komt. Hoe verder het geluid zich van de bron af beweegt, des te zachter wordt het geluid. Dat is als volgt te verklaren:
Op enig moment geeft de bron een geluid af met een bepaalde intensiteit. Dit geluid met deze intensiteit heeft in totaal een bepaalde hoeveelheid energie die zich als een ballon rondom de bron bevindt. Dit kan als het ware worden voorgesteld als de wand van de ballon.Het geluid plant zich voort in alle richtingen. Dus als er op een later tijdstip wordt gekeken, dan is de ballon rondom de bron groter geworden. Maar de wand van de ballon bevat nog steeds dezelfde hoeveelheid energie, die nu over een groter oppervlak verdeeld moet worden. Dus wordt de wand overal steeds dunner als de afstand tot de bron verder toeneemt.
De oppervlakte van een bol kan berekend worden met formule 5. De oppervlakte van de bol is dus afhankelijk van het kwadraat van de straal van de bol. Deze straal van de bol is hier de afstand tussen de geluidsbron en het meetpunt.
A = 4.πr2
Formule 5: Berekening van de oppervlakte van een bol
Een voorbeeld maakt een en ander duidelijk:
Een geluidsbron met een vermogen van 0,1 W produceert een constant geluid. Uit formule 5 volgt dat op een afstand van 1 meter (r in de formule) deze hoeveelheid energie verdeeld wordt over een oppervlakte van 4 x 3,14 x 12= 12,57 m2. De geluidsintensiteit (in W/m2) is dan te berekenen door het vermogen van de bron (0,1 W) te delen door de oppervlakte van de (virtuele) bol:12,57 m2.
I = 0,1 W /12,57 m2 = 0,008 W/m2
Met behulp van formule 2 kan dit worden omgezet naar decibel:
LI = 10.log(0,008/10-12).
Daaruit volgt:
LI = 10.log(8.109)
En nog verder:
LI = 10 x 9,9 = 99 dB
De afname van 20 dB bij vertienvoudiging van de afstand laat zich als volgt verklaren:
Bij berekening van de oppervlakte van de bol wordt de afstand in het kwadraat genomen. Het kwadraat van 10 is gelijk aan 100.
Bij omrekening naar decibel wordt daar de logaritme van genomen. En dat wordt vermenigvuldigd met 10. De logaritme van 100 is 2.
Vermenigvuldigd met 10 is dat 20.
De afname van 20 dB bij vertienvoudiging komt dus omdat 10.log 100 = 20.
Bij een afstand van 2 meter tot de bron wordt deze hoeveelheid energie verdeeld over de oppervlakte van de virtuele bol van 4 x 3,14 x 22
= 50,27 m2. Het vermogen van de bron is nog steeds 0,1 W. De geluidsintensiteit is bij een afstand van 2 meter tot de bron te berekenen als:Bij berekening van de oppervlakte van de bol wordt de afstand in het kwadraat genomen. Het kwadraat van 10 is gelijk aan 100.
Bij omrekening naar decibel wordt daar de logaritme van genomen. En dat wordt vermenigvuldigd met 10. De logaritme van 100 is 2.
Vermenigvuldigd met 10 is dat 20.
De afname van 20 dB bij vertienvoudiging komt dus omdat 10.log 100 = 20.
I = 0,1 W /50,27 m2 = 0,002 W/m2
Ook dit kan weer omgezet worden naar decibel:
LI = 10.log(0,002/10-12).
Daaruit volgt:
LI = 10.log(2.109)
En nog verder:
LI = 10 x 9,3 = 93 dB
Hier is de afstand verdubbeld van 1 meter naar 2 meter. Het resultaat is een afname van 6 dB. Maar er is ook een verschil van 6 dB als de afstand toeneemt van 2 meter naar 4 meter, of van 100 meter naar 200 meter. Een verdubbeling van de afstand tot de bron van het geluid geeft in het vrije veld dus een afname van 6 dB. Klik op het ikoontje hiernaast voor een berekening van de luidheid op een andere afstand dan 1 en 2 meter. Als er een willekeurige afstand wordt ingevuld en daarna het dubbele van deze afstand, dan is de luidheid op deze dubbele afstand telkens 6 dB minder. Er is hiermee ook te berekenen dat bij vertienvoudiging van de afstand de luidheid met 20 dB afneemt.
Resonantie
De hierboven staande berekeningen en theorie gaan op voor het vrije veld, als er geen enkel obstakel is. Een lopende golf bestaat alleen maar zolang er geen oppervlak is waartegen het geluid botst. Zodra geluid een oppervlak zoals een muur tegenkomt, zal het erdoor weerkaatst worden, vergelijkbaar met een bal die tegen de muur gegooid wordt. Dat gebeurt in een concertzaal, in een kamer, maar ook in de gehoorgang. Dit weerkaatste geluid gaat samen met het inkomende geluid. Er treedt een interactie op tussen het inkomende geluid en het weerkaatste geluid. Wat het resultaat daarvan is, is afhankeljk van de golflengte (en dus de frequentie) van het geluid. Beide geluidsgolven kunnen elkaar versterken, maar ze kunnen elkaar ook uitdoven. En alleswat daartussen zit. Bij frequenties waarbij de geluidsgolven elkaar precies opheffen of uitdoven ontstaat een staande golf.
Bij een staande golf bevinden de punten van de sinus zich altijd op dezelfde plaats in de ruimte. Er zijn daarbij twee belangrijke punten aan te wijzen:de knopen en de buiken. Op plekken waar zich een knoop bevindt, doven de twee geluidsgolven elkaar uit. Op plaatsen waar zich een buik bevindt, versterken de twee golven elkaar maximaal.
Figuur 2: Het ontstaan van een staande golf.
In figuur 2 is een heengaande sinus getekend (blauw) en een teruggekaatste sinus (rood). Door de waarde van deze beide sinussen bij elkaar op te tellen, ontstaat de resultante, de paarse lijn. In de beginstand ligt de paarse lijn op de nullijn, want op elke plaats is de ene golf net zoveel positief als de andere golf negatief is, en andersom. Door de sinussen te verschuiven ontstaan er verschillen in de optelsom en verandert de paars lijn van vorm. Maar het is duidelijk dat op bepaalde plaatsen de optelsom altijd gelijk is aan nul. Dat zijn de knopen (klik op de button om deze te zien). Op andere plaatsen is de optelsom steeds maximaal (of minimaal), daar is een buik (klik op de button om deze te zien).
Een hele golflengte van de staande golf bevindt zich in deze figuur tussen de twee buitenste "buiken". Maar ook bij de andere posities van de heengaande sinus is dit steeds een hele golflengte met de nulpunten en de maxima en minima op dezelfde plaats. Ook bij de lopende golf kan de golflengte worden bepaald. Maar bij een lopende golf is er geen sprake van knopen en buiken. Daar wordt de golflengte bepaald door te meten tussen een bepaald punt (bijvoorbeeld een doorgang door de nullijn van beneden naar boven) en het eerstvolgende punt waar dat ook weer optreedt. Merk op dat de golflengte van de staande golf gelijk is aan de golflengte van de lopende golven die deze staande golf hebben gemaakt.
Muziekinstrumenten maken ook gebruik van staande golven en resonanties. Daarom is in figuur 3 van een aantal instrumenten een voorbeeld gegeven van de manier waarop resonanties en de daaruit voorkomende staande golven hierbij worden gebruikt.
Figuur 3: Verschillende soorten muziekinstrumenten gebruiken verschillende effecten van resonantie.
Staande golven komen ook voor in een aantal situaties waar de audicien mee te maken heeft, zoals in tabel 2 hieronder wordt opgesomd.
- Vlak bij een muur bij IG-meting met een zuivere toon (sweeptone).
- Door de weerkaatsing van de golven tegen de muur wordt de inkomende geluidsgolf beïnvloedt. Daarom moet de proefpersoon bij deze meting niet te dicht bij de muur zitten. Op enige afstand van de muur heeft het geen effect meer.
- In de hoortoestelslang bij de open aanpassing, van luidspreker tot dome.
- Deze situatie wordt gezien als een buis die aan twee zijden open is. Het is duidelijk dat het uiteinde van de slang open is,maar ook de kant waar de luidspreker zich bevindt, wordt beschouwd als een open einde. Dit heeft consequenties voor het aantal en de frequenties van de resonantiepieken.
- In de toonbocht en slang bij een aanpassing met oorstukje, van luidspreker tot het einde van het oorstukje.
-
Ook deze situatie kan worden beschouwd als een buis die aan twee zijden open is. Dat er in deze situatie en bij de aanpassing met een dunne slang
resonantiepieken ontstaan, kan het best geïllustreerd worden met een frequentiekarakteristiek van een hoortoestel.
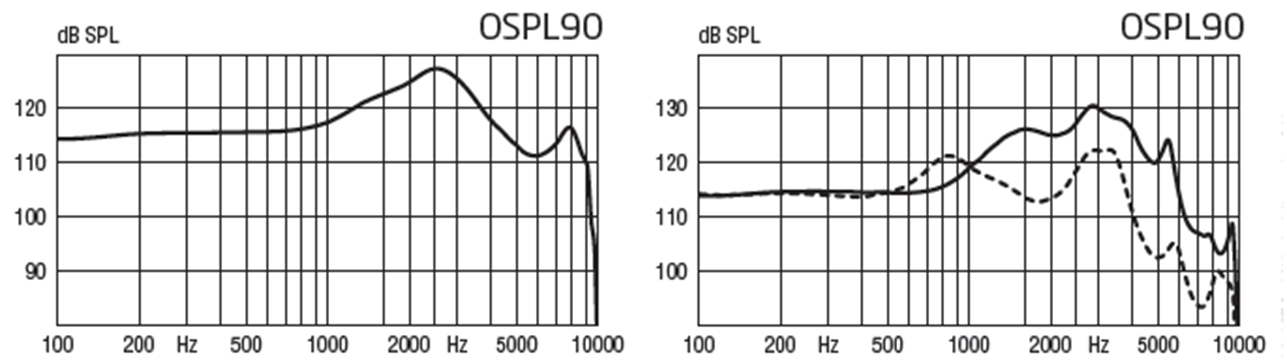
Figuur 4: De OSPL90 karakteristiek van de Oticon Alta. Links: miniRITE 85, rechts: miniBTE 85.
In figuur 4 is te zien dat de linker grafiek slechts twee pieken heeft. Dit is voor de versie met de luidspreker in het oor. Het geluid gaat dus niet eerst door een slang, maar komt direct in de gehoorgang. Daardoor kunnen er geen resonaties in die slang optreden. De pieken die er wel zijn, zijn de resonantiepieken van de telefoon.
De rechter figuur heeft twee grafieken. De stippellijn is voor de versie met de dunne slang, de doorgetrokken lijn is voor de aanpassing met een oorstukje. In deze grafieken zijn meer pieken te zien. Deze extra pieken zijn de resonantiefrequenties die ontstaan in de slang tussen de telefoon en het uiteinde van het oorstukje of de dome.
Bron:C.L. Moryl, C.L.;Danhauer, J.L.;DiBartolomeo, J.R.: Real Ear Unaided Responses in
Ears with Tympanic Membrane Perforations. J. Am. Acad. Audiol 3: 60 – 65(1992) -
Ook deze situatie kan worden beschouwd als een buis die aan twee zijden open is. Dat er in deze situatie en bij de aanpassing met een dunne slang
resonantiepieken ontstaan, kan het best geïllustreerd worden met een frequentiekarakteristiek van een hoortoestel.
- In de open gehoorgang, zonder oorstukje.
-
Dit is natuurlijk gelijk aan een buis die aan een zijde is afgesloten. Het trommelvlies fungeert dan als afsuiter.
-
Omdat het trommelvlies de afsluitende kant is, verandert er dus wel iets aan de resonanties als er sprake is van een perforatie van het
trommelvlies. Afhankelijk van de grootte van de perforatie sluit het trommelvlies de gehoorgang aan die zijde meer of minder af en veranderen de
resonanties, zoals in
figuur 5 is te zien.
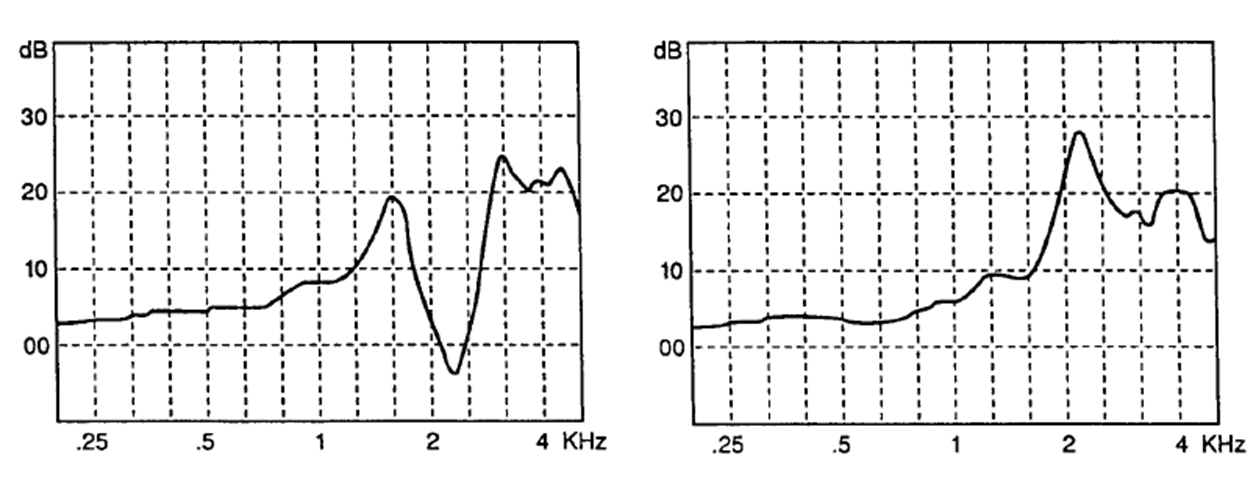
Figuur 5: De REUG gemeten bij een grote trommelvliesperforatie (links). Rechts is de REUG van hetzelfde oor nadat de perforatie operatief is gesloten.
De meting links toont het kenmerkende beeld van een REUG bij een grote perforatie. Er worden twee pieken gemeten gescheiden door een dal met een diepte van ongeveer 10 dB.
-
Omdat het trommelvlies de afsluitende kant is, verandert er dus wel iets aan de resonanties als er sprake is van een perforatie van het
trommelvlies. Afhankelijk van de grootte van de perforatie sluit het trommelvlies de gehoorgang aan die zijde meer of minder af en veranderen de
resonanties, zoals in
figuur 5 is te zien.
-
Dit is natuurlijk gelijk aan een buis die aan een zijde is afgesloten. Het trommelvlies fungeert dan als afsuiter.
- In de gehoorgang, afgesloten met een oorstukje.
-
Deze situatie kan op twee manieren worden bekeken:
- Als het hoortoestel is uitgeschakeld, is het een buis die aan twee zijden is afgesloten.
- Als het hoortoestel is ingeschakeld, is het een buis die aan een zijde afgesloten is. De open kant is dan de kant waar het oorstukje zit. Daar kom het geluid uit. Dit is vergelijkbaar met de telefoon van het hoortoestel aan het begin van de toonbocht.
-
Deze situatie kan op twee manieren worden bekeken:
- In de gehoorgang, afgesloten met een gehoorbeschermer.
- In dit geval is er sprake van een buis die aan twee zijden is afgesloten.
Om te berekenen in welke frequentie een snaar trilt (en dus welke toon
wordt geproduceerd) moet de volgende formule worden gebruikt:
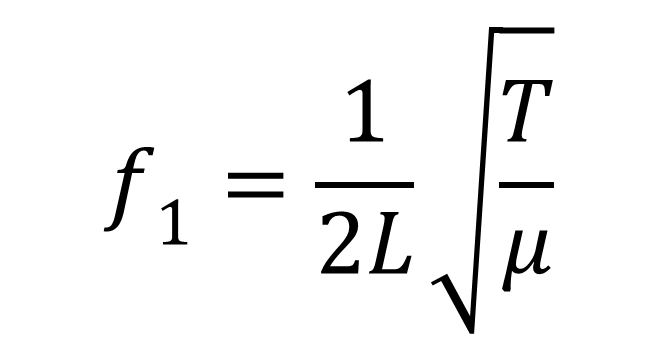
Daarbij geldt:
L = de lengte van de snaar (meter)
T = spanning in de snaar (Newton)
μ = gewicht per lengte-eenheid (kilogram / meter)
Staande golf in een snaarwordt geproduceerd) moet de volgende formule worden gebruikt:
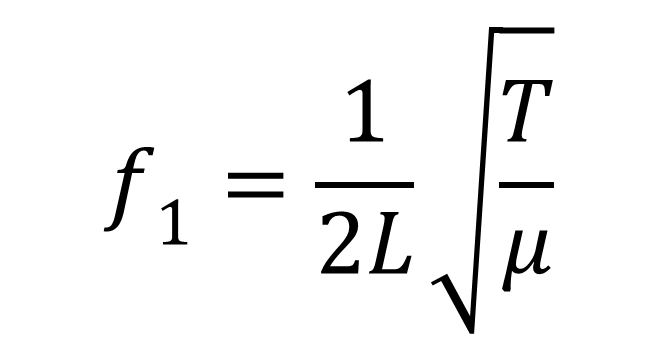
Daarbij geldt:
L = de lengte van de snaar (meter)
T = spanning in de snaar (Newton)
μ = gewicht per lengte-eenheid (kilogram / meter)
Het is mogelijk om te berekenen bij welke frequentie er resonantie optreedt in tabel 2 beschreven situaties. Om te beginnen wordt de golflengte van de resonantie van een snaar berekend. Een snaar van een viool of een harp is aan beide zijden vast. De uiteinden kunnen dus niet bewegen en fungeren bij resonanties als een knoop. Bij staande golven (want daar gaat het hier over) is er altijd een afwisseling van buiken en knopen. Er zit altijd een buik tussen twee knopen of een knoop tussen twee buiken. Zie hiervoor figuur 2.
In zijn eenvoudigste vorm van een staande golf in de snaar is er een buik tussen twee knopen. Dat is dus een halve golflengte.Deze eerste situatie is de grootste golflengte waarbij een resonantie optreedt. Er treedt namelijk niet slechts bij één golflengte resonantie op, ook bij kleinere golflengtes treedt resonantie op. Dat is te zien door op het ikoontje hiernaast te klikken. Er verschijnt dan een scherm waarin de eerste acht harmonischen in een snaar worden getoond. Daar is te zien dat er bij de eerste harmonische nog maar een halve golflengte in de snaar past, maar dat er bij elke hogere harmonische steeds een halve golflengte bij komt. Ook is te zien dat de amplitude van de hogere harmonischen steeds iets kleiner wordt. Ook de golflengtes van deze hogere harmonischen kunnen berekend worden.
De golflengte waarbij resonanties in een snaar ontstaan, zijn niet alleen afhankelijk van de lengte van de snaar, maar ook van de spanning en het gewicht van de snaar. Voor het gemak worden deze factoren even buiten de berekening gehouden.
Van de eerste harmonische past een halve golflengte in de snaar. Dan is de golflengte van de eerste harmonische te berekenen met formule 6
λ=2.L
Formule 6: Berekening van de golflengte van de eerste harmonische
De "L" in deze formule is de lengte van de snaar. Bij de tweede harmonische past er een hele golflengte in de snaar. Uitgaand van formule 6 moet daar een aanpassing aan gemaakt worden (formule 7). De golflengte is nu de helft van die van de eerste harmonische. Dus wordt de formule:
λ=2.L / 2
Formule 7: Berekening van de golflengte van de tweede harmonische
De "twee" waardoor gedeeld wordt in deze formule is het nummer van de harmonische.
Bij de derde harmonische past er anderhalve golflengte in de snaar en moet formule 6 worden gedeeld door drie om de golflengte te berekenen. Deze drie is weer het nummer van de golflengte. Het is dus mogelijk om een algemene formule op te stellen om de golflengte van de hogere harmonischen te berekenen (formule 8):
λ=2.L / n
Formule 8: Berekening van de golflengte van de harmonischen in een snaar.
In deze formule is "L" de lengte van de snaar (in meter) en is "n" het nummer van de harmonische waarvan de golflengte berekend moet worden. De berekening van de golflengtes van de harmonischen is de basis voor de berekening van de frequentie die door de trillende snaar wordt voortgebracht. Maar omdat dat bij een snaar van meerdere factoren afhankelijk is, wordt hier niet verder uitgelegd hoe de frequenties van de hogere harmonischen hier worden berekend.
Staande golf in een open buis
Het uitgangspunt is:
2.L / n = v / f
De frequentie moet met deze formule berekend kunnen worden. Door "f" naar de andere kant te brengen wordt het:
f . (2L/n) = v
Nu delen door (2L/n). "Delen door een breuk is vermenigvuldigen met het omgekeerde". Dus dit levert:
f = v. (n /2L).
Na herschikking wordt het uiteindelijk:
f = n.v /2L.
De situatie van resonanties in een buis die aan twee zijden open is, heeft veel overeenkomsten met de resonanties in een snaar. In een snaar zijn de
buitenzijden vast en dus een knoop, met een buik in het midden. Bij een buis die aan beide zijden open is, vormen de zijden een buik, terwijl er zich een
knoop in het midden bevindt.
Door op het ikoontje hiernaast te klikken worden de verschillende harmonischen in een aan twee zijden open buis getoond. Het is wat minder makkelijk te zien,
maar ook hier bestaat de eerste harmonische uit een halve golflengte. Ter vergelijking kan eventueel door
HIER te klikken nogmaals het scherm met de harmonischen van een snaar worden opgeroepen.
2.L / n = v / f
De frequentie moet met deze formule berekend kunnen worden. Door "f" naar de andere kant te brengen wordt het:
f . (2L/n) = v
Nu delen door (2L/n). "Delen door een breuk is vermenigvuldigen met het omgekeerde". Dus dit levert:
f = v. (n /2L).
Na herschikking wordt het uiteindelijk:
f = n.v /2L.
Omdat de staande golf in een buis op eenzelfde manier verandert als in een snaar, is de formule precies hetzelfde, dus zoals in formule 8.
Omdat in een buis de staande golf geen beweging van een snaar is, maar een beweging van de lucht, is het nu wel mogelijk om de frequentie te berekenen waarbij de staande golven ontstaan in een buis die aan beide zijden open is. In formule 4 wordt de formule weergegeven om uit de frequentie en de snelheid van het geluid te berekenen wat de golflengte is. Deze formule is:
λ = v / f
In formule 8 wordt ook een formule gegeven om de golflengte te berekenen:
λ=2.L / n
Omdat beide formules een methode zijn om de golflengte te berekenen, kunnen deze formules worden gecombineerd.
2.L / n = v / f
Door deze berekening te bewerken ontstaat uiteindelijk formule 9
fn = n.v / 2L
Formule 9: Berekening van de frequentie van de harmonischen in een aan twee zijden open buis.
Hierbij is "f" de frequentie (in Hz), "n" is het nummer van de harmonische, "v" is de snelheid van het geluid (343 m/s) en "L" is de lengte van de buis (in meter).Met deze formule kan nu bijvoorbeeld de resonantiefrequentie worden berekend zoals die optreedt in de dunne slang van een open aangepast hoortoestel.
De lengte van een dunne slang is in dit geval gelijk aan 48 mm (=0,048 m) Wat is nu de resonantiefrequentie van de eerste harmonische?
Als de gegevens in formule 9 worden ingevoerd, dan leidt dat tot:
f1 = 1.343 / 2. 0,048
Verder uitgewerkt:
f1 = 343 / 0,096 = 3573 Hz
De resonantiefrequentie van de eerste harmonische bij een slang met een lengte van 48 mm is dus 3573 Hz. Dat valt ruim binnen het hoorbare gebied. Bij de aanpassing van een hoortoestel moet er dus rekening gehouden worden met de extra natuurlijke versterking van het geluid rondom deze frequentie. Dat hoeft de audicien niet te doen, de hoortoestelfabrikanten hebben dat al verwerkt in hun aanpasprogramma.
Door in formule 9 voor "n" een 1 in te vullen wordt de frequentie van de eerste harmonische ofwel de grondfrequentie berekend. Dus met formule 10 wordt de frequentie van de eerste harmonische beschreven:
f1 = v / 2L
Formule 10: Berekening van de frequentie van de eerste harmonische in een aan twee zijden open buis.
Door formule 10 te combineren met formule 9 ontstaat er een gemakkelijke formule om de frequenties van de hogere harmonische te berekenen (formule 11).
fn = n. f1
Formule 11: Berekening van de frequentie van de harmonischen met behulp van de frequentie van de eerste harmonische.
Het uitgangspunt is:
4/(2n-1) . L = v / f
De frequentie moet met deze formule berekend kunnen worden. Door "f" naar de andere kant te brengen wordt het:
f . 4/(2n-1) . L = v
Nu delen door 4/(2n-1). "Delen door een breuk is vermenigvuldigen met het omgekeerde". Dus dit levert:
f . L = v. (2n-1)/4
Nu nog delen door "L". f = v . (2n-1)/4L
Na herschikking wordt het uiteindelijk:
f = (2n-1) . v /4L
Staande golf in een half open buis4/(2n-1) . L = v / f
De frequentie moet met deze formule berekend kunnen worden. Door "f" naar de andere kant te brengen wordt het:
f . 4/(2n-1) . L = v
Nu delen door 4/(2n-1). "Delen door een breuk is vermenigvuldigen met het omgekeerde". Dus dit levert:
f . L = v. (2n-1)/4
Nu nog delen door "L". f = v . (2n-1)/4L
Na herschikking wordt het uiteindelijk:
f = (2n-1) . v /4L
Bij de half-open buis is er een open einde met dus bij een staande golf een buik aan die zijde. Bij de gesloten zijde aan de andere zijde is er een knoop. Dat is te zien door op het ikoontje hiernaast te klikken. In het scherm vormt de rechterkant de gesloten zijde, de linkerkant is de open zijde.
Bij het ontstaan van de eerste harmonische past er maar een kwart golflengte in deze buis. Bij de tweede harmonische moet er weer een knoop aan de gesloten zijde zijn en een buik aan de open zijde. Dat kan pas weer als er driekwart sinus in de half-open buis past. Vergelijk de resonanties in een buis die aan twee zijden open is met de resonanties in een buis die aan één zijde open is door HIER te klikken.
De formule om de lengte van de golf bij de verschillende resonantiefrequenties te berekenen ziet er als volgt uit (formule 12)
λn = 4 /(2n-1) . L
Formule 12: Berekening van de golflengte van de harmonischen bij een half-open buis.
De factor (2n-1) heeft altijd een oneven getal als uitkomst. Dat is nodig omdat er telkens een oneven aantal "kwart golflengtes" in de half-open buis passen bij het ontstaan van een staande golf. Omdat er hier weer sprake is van een trilling van de lucht, kunnen ook hier weer realtief gemakkelijk de frequenties worden uitgerekend waarbij de resonanties optreden (formule 13).
fn = (2n-1) . v /4L
Formule 13: Berekening van de frequentie van de harmonischen bij een half-open buis.
Met deze formule kan de eerste resonantiefrequentie worden berekend die optreedt in de gehoorgang, die immers ook een half-open buis is.
De lengte van de gehoorgang is bij de man ongeveer 28 mm (0,028 m), de snelheid van het geluid (v) = 343 m/s en n is 1, omdat de eerste harmonische wordt berekend. Invoeren in formule 13 geeft:
f1 = (2.1-1) . 343 /(4 . 0,028)
Een eerste uitwerking levert:
f1 = (2-1) . 343 /0,112
En verder:
f1 = 343 /0,112 = 3063 Hz.
Met enige moeite kan deze resonantiefrequentie worden teruggevonden bij het meten van de REUR of de REUG. Bij deze meting wordt de resonantie van de open gehoorgang gemeten en daar is deze net berekende frequentiete zien. Maar er speelt meer mee dan alleen de resonantie van de buis. De wand van de gehoorgang is zacht en absorbeert een beetje van het geluid. Ook het trommelvlies trilt bij aanbieden van geluid en dat heeft ook een effect. Als laatste worden er ook resonanties van de oorschelp en andere structuren rond het oor gemeten die de uiteindelijke vorm van de REUR / REUG bepalen (zie figuur 6).
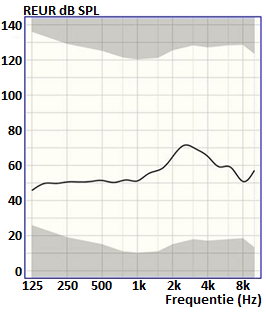
Figuur 6: De bij de REUR gemeten piek kan in principe ongeveer berekend worden met de formule voor een half open buis.
Nu is alleen de eerste resonantiefrequentie berekend. Door goed te kijken naar formule 13, is te zien dat de tweede resonantiefrequentie (of elke andere hogere harmonische) berekend kan worden door de hier gevonden resonantiefrequentie te vermenigvuldigen met (2n -1). Voor de tweede resonantiefrequentie is dat dus (2.2 - 1) = 3. De frequentie van de tweede harmonische is dus 3 x 3063 Hz = 9189 Hz. Deze frequentie wordt meestal niet gemeten en ligt ook nog eens buiten het bereik van veel hoortoestellen. De tweede en hogere harmonischen zijn dus eigenlijk niet van belang bij de aanpassing van een hoortoestel. De grootte en plaats van de eerste harmonische is wel van belang bij een hoortoestelaanpassing. Elke rekenregel houdt hier dan ook rekening mee.
Staande golf in een gesloten buis
Bij een afgesloten buis is er aan beide zijden een afsluiting en dus is er bij een staande golf in deze gesloten buis aan beide zijden een knoop. Deze situatie is vergelijkbaar met de situatie van een snaar en dus is ook de formule hier hetzelfde. Een aan beide zijden gesloten buis komt voor bij een door een oorstukje afgesloten gehoorgang als het hoortoestel niet aan staat. Ook bij gebruik van gehoorbescherming treedt dit op. Deze resonantiefrequentie is te berekenen met formule 9 door uit te gaan van een lengte van 13 mm bij een door een oorstukje afgesloten gehoorgang:
f1 = 1.343 / 2. 0,013
Verder uitgewerkt:
f1 = 343 / 0,026 = 13.192 Hz
Deze frequentie is zo hoog dat dit nauwelijks opgemerkt wordt. Het occlusie-effect dat in deze situtaie optreedt is veel groter en staat hier dan ook op de voorgrond.
Luidheid van de hogere harmonischen
Het is ook mogelijk om de luidheid van de hogere harmonischen te berekenen. De luidheid van deze hogere harmonischen wordt dan uitgedrukt als een percentage of gedeelte van de luidheid van de eerste harmonische. De formule om de luidheid van harmonischen te berekenen is formule 14:
In = 1 / n
Formule 14: Berekening van de luidheid van de harmonischen.
Als in deze formule het nummer van de harmonsche wordt ingevuld, dan is de intensiteit (I) van de eerste harmonische 1/1, dus 100%. de intensiteiet van de tweede harmonicshe is 1/2, dus 50% van de intensiteit van de eerste harmonische. Op gelijke wijze is de luidheid van de hogere harmonischen uit te rekenen. De luidheid van de hogere harmonischen neemt snel af ten opzichte van de eerste harmonische, en ook de frequenties van de hogere harmonischen zijn veel hoger. Daardoor neemt het belang van de hogere harmonischen snel af. Voor de herkenbaarheid van klinkers bijvoorbeeld, zijn eigenlijk alleen de eerste en de tweede harmonische van belang.
Uit de formule voor de berekening van de kracht valt af te leiden dat de eenheid voor kracht gelijk is aan
kg.m/s2. Toch wordt deze eenheid nergens gebruikt. In plaats daarvan wordt voor kracht de eenheid Newton (N) gebruikt. Dat is vooral veel gemakkelijker.
Deze twee eenheden zijn precies gelijk: 1 N = 1 kg.m/s2.
Krachtkg.m/s2. Toch wordt deze eenheid nergens gebruikt. In plaats daarvan wordt voor kracht de eenheid Newton (N) gebruikt. Dat is vooral veel gemakkelijker.
Deze twee eenheden zijn precies gelijk: 1 N = 1 kg.m/s2.
Elke start van een beweging vergt een bepaalde hoeveelheid kracht. Dus ook het in beweging brengen van de gehoorbeentjes, ook al is de kracht die nodig is om de gehoorbeenketen te laten bewegen zeer klein. Inzicht in de manier waarop "kracht" werkzaam is in de keten van het horen geeft inzicht in de normale werking van het gehoor en daardoor dus ook inzicht in de gevolgen bij niet goed functioneren van bepaalde onderdelen van het hoorsysteem.
Met behulp van formule 15 kan uitgerekend worden welke kracht nodig is om een bepaalde massa in beweging te krijgen, of hoeveel kracht een voorwerp uitoefent op de ondergrond. Bij deze formule kan heel goed gedacht worden aan een gewicht dat bijvoorbeeld op een tafel staat. Dat gewicht, uitgedrukt in kilogram, kan worden omgerekend naar een kracht in Newton met behulp van formule 15.
F= m.a
Formule 15: Berekening van de kracht die een gewicht uitoefent op een oppervlakte.
In deze formule is de "F" (van het Engelse Force) het symbool voor "Kracht" met als eenheid de Newton (N). Met "m" wordt de massa van een voorwerp aangeduid, uitgedrukt in kilogram (kg). De "a" komt van het Engelse acceleration, wat versnelling betekent. De eenheid van versnelling is meter per secondekwadraat (m/s2). Deze versnelling kan alle kanten op gericht zijn. Voor een versnelling naar beneden, zoals bij een gewicht dat op een tafel staat, wordt de versnelling van de zwaartekracht genomen. Dit is een constante. De versnelling van de zwaartekracht (weergegeven met de letter "g" van het Engelse gravity) bedraagt 9,81 m/s2.
Een gewicht van 10 kg oefent op het oppervlak waar het op staat dus een kracht uit van :
F= m.a = 10 kg x 9,81 m/s2 = 98,1 kg.m/s2 = 98,1 N
Als op deze manier de kracht wordt berekend die door een voorwerp op een oppervlak wordt uitgeoefend, dan is dat dus het gewicht. Strikt genomen wordt het gewicht van iets dus uitgedrukt in Newton. Als gezegd wordt dat iets 5 kilo weegt, dan wordt daar in de natuurkunde niet het gewicht, maar de massa onder verstaan.
Druk
In het deel over de luidheid van geluid werd al aangegeven dat geluid bestaat uit zeer kleine luchtdrukvariaties ten opzichte van de heersende luchtdruk. Doordat deze drukvariaties tegen het trommelvlies botsen, worden geluiden waargenomen. Deze geluidsdruk oefent een kracht uit op het trommelvlies, waarna het via de gehoorbeenketen wordt doorgegeven naar de cochlea. Druk kan worden omschreven als "Kracht per oppervlakte". Dat is ook de manier waarop druk kan worden berekend (formule 16):
P= F/A
Formule 16: Berekening van de druk
In deze formule staat de "F" weer voor "Kracht". De eenheid hiervan is Newton (N). De "A" komt van het Engelse Area en duidt de oppervlakte aan. De eenheid is vierkante meter (m2). De "P" (van het Engelse Pressure) wordt gebruikt wordt voor de druk. De eenheid van druk kan uit de formule worden afgeleid en is gelijk aan Newton per vierkante meter (N/m2). In plaats van N/m2 kan ook de eenheid Pascal (Pa) worden gebruikt, bij het gebruik van deze eenheid hoeft een en ander niet omgerekend te worden, 1 Pa = 1 N/m2.
Wat zijn de consequenties van de definities van druk en kracht? Dat is misschien het beste uit te leggen aan de hand van het volgende voorbeeld.

Figuur 7: Hetzelfde blok, driemaal op aan andere manier rechtop gezet.
In figuur 7 is hetzelfde blok drie keer op een andere manier neergelegd. Het blok heeft 2 groene zijden van 20 x 40 cm, twee rode zijden van 10 x 40 cm en twee blauwe zijden van 10 x 20 cm. De afmetingen van dit blok zijn dus 10 x 20 x 40 cm. Het gewicht van dit blok is gelijk aan 600 N. Dit is dus de kracht die dit blok op de ondergrond uitoefent.
Hoeveel druk er wordt uitgeoefend is afhankelijk van het oppervlak dat contact maakt met de ondergrond. Hieronder is dit berekend voor de drie situaties van figuur 7
-
In de eerste situatie ligt het blok op een groene zijde. De kracht van 600 N drukt op een oppervlak van 0,2 x 0,4 = 0,08 m2.
Dus is in deze situatie de druk
P= F/A = 600 / 0,08 = 7.500 N/m2 = 7.500 Pa.
-
In de tweede situatie ligt het blok op een rode zijde. De kracht van 600 N drukt op een oppervlak van 0,1 x 0,4 = 0,04 m2.
Dus is in deze situatie de druk
P= F/A = 600 / 0,04 = 15.000 N/m2 = 15.000 Pa.
-
In de derde situatie ligt het blok op een blauwe zijde. De kracht van 600 N drukt op een oppervlak van 0,1 x 0,2 = 0,02 m2.
Dus is in deze situatie de druk
P= F/A = 600 / 0,02 = 30.000 N/m2 = 30.000 Pa.
Het oppervlakte effect
Van dit principe wordt gebruik gemaakt in het middenoor. In het middenoor wordt de geluidsdruk die bij het trommelvlies aankomt, door de gehoorbeentjes doorgegeven naar het veel kleinere ovale venster. Hoe werkt dat?
Figuur 8a: Het vlak waar druk op wordt uitgeoefend.
In figuur 8 is een vlak getekend. Als op dit figuur wordt geklikt, komt figuur 8b tevoorschijn.
Daarin is te zien dat er een druk van 600 Pa op dit vlak wordt uitgeoefend. De oppervlakte van het vlak wordt gesteld op 0,2 m2.
In figuur 8c is te zien dat de druk aan de ene kant van het vlak aan de andere kant van het vlak een kracht veroorzaakt. De grootte van die kracht is te berekenen met een variant op formule 16:
P= F/A ⇔ F= P.A
Formule 17: Door formule 16 iets anders op te schrijven kan vanuit de druk de kracht worden berekend.
Een druk van 600 N op een oppervlakte van 0,2 m2 leidt tot een kracht van:
F= P x A = 600 x 0,2 = 120 N
Deze kracht wordt in figuur 8d door een vaste verbinding doorgegeven naar het volgende vlak. Aan de rechter zijde van dit vlak (de donkerrode kant) kan vanuit deze kracht weer worden uitgerekend wat de druk is die dit vlak uitoefent op de omgeving:
P= F / A = 120 / 0,2 = 600 Pa
Het is niet verwonderlijk dat in dit geval de druk weer precies even groot is als er aan het begin op het linker oppervlak werd uitgeoefend, beide vlakken zijn immers even groot.
Het wordt anders als, zoals in figuur 8e, het tweede vlak kleiner wordt. Het eerste vlak en de druk die er op uitgeoefend wordt, is hetzelfde gebleven. Daardoor is de kracht die ontstaat ook hetzelfde: 120 N. De oppervlakte van het tweede vlak is nu nog maar 0,05 m2. Als nu de resulterende druk wordt uitgerekend levert dit:
P= F / A = 120 / 0,05 = 2400 Pa
De druk is hier dus groter geworden, omdat het oppervlak waar het naar toe is overgebracht kleiner is geworden.
Bij nadere beschouwing is de druk vier keer zo groot geworden van 600 N naar 2400 N en is het oppervlak vier keer zo klein geworden (van 0,2 m2 naar 0,05 m2). Daartoe moest de druk wel eerst worden omgezet naar een kracht, waarna de kracht weer werd omgezet naar druk. In een berekening ziet dat er zo uit:
P1 . A1 = F = P2 . A2
Vanuit de eerste druk (P1) op het eerste vlak (A1) ontstaat een kracht. Diezelfde kracht wordt doorgegeven naar het tweede vlak (A2), waardoor er een nieuwe druk (P2) ontstaat.
In feite staat er hierboven drie keer dezelfde waarde, alleen telkens iets anders weergegeven. Als uit de vergelijking hierboven de kracht wordt weggelaten, dan staat er:
P1 . A1 = P2 . A2
Door dit geheel nog iets anders neer te zetten, ontstaat er een formule waarmee de verandering van de druk kan worden berekend als bekend is wat de grootte van de twee vlakken is:
P2 = A1 /A2 .P1
Formule 18: De druk op het tweede vlak is te berekenen als de verhouding van de beide oppervlakken bekend is.
Hierboven wordt er een verhouding tussen de twee betrokken oppervlakken berekend. Dat kwam ook al naar voren in het rekenvoorbeeld. Met formule 18 is in het algemene geval te berekenen wat de vergroting van de druk wordt als deze druk wordt doorgegeven naar een kleiner oppervlak. Andersom blijkt daar ook uit dat de druk lager wordt als er van een klein oppervlak wordt overgegaan naar een groot oppervlak.
In het middenoor is een soortgelijke situatie als hierboven beschreven te vinden. Geluid treft als een drukgolf het trommelvlies. Deze druk wordt door de gehoorbeentjes doorgegeven aan het kleinere ovale venster, in figuur 9 wordt deze verbinding tussen het trommelvlies en het ovale venster getoond.
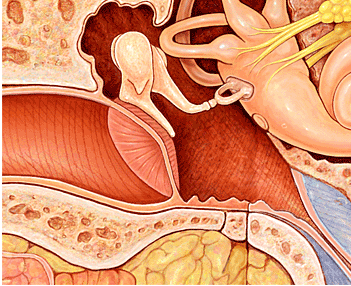
Figuur 9: Het middenoor, waar het trommelvlies middels de gehoorbeentjes in contact staat met het ovale venster.
De oppervlakte van het trommelvlies (ATV) is ongeveer 60 mm2. De oppervlakte van het ovale venster (AOV) bedraagt ongeveer 3 mm2. Als dit gegeven in formule 18 wordt ingevoerd, dan geeft dat aan hoeveel groter de druk wordt:
P2 = ATV /AOV .P1 ⇒ P2 = 60 / 3 .P1 ⇒ P2 = 20 P1
De druk die op het trommelvlies wordt uitgeoefend (P1) wordt dus met een factor 20 versterkt doorgegeven aan het ovale venster (P2) als gevolg van de verhouding van beide oppervlakken.
De hefboomwerking
De berekening van de versterking van de druk zoals hierboven weergegeven, gaat er van uit dat er een eenvoudige overdracht van de druk plaatsvindt. Maar, zoals in figuur 9 is te zien, is de gehoorbeenketen niet een eenvoudige rigide rechte verbinding tussen het trommelvlies en het ovale venster. De gehoorbeenketen is niet recht en de verbindingen tussen de gehoorbeentjes onderling zijn beweeglijk. Deze opstelling heeft nog een extra versterkend effect: het hefboom-effect.
Bron:http://gtjournal.tadl.org
De natuurkundige berekening bij de hefboom berusten op de effecten van krachten rondom een draaipunt.
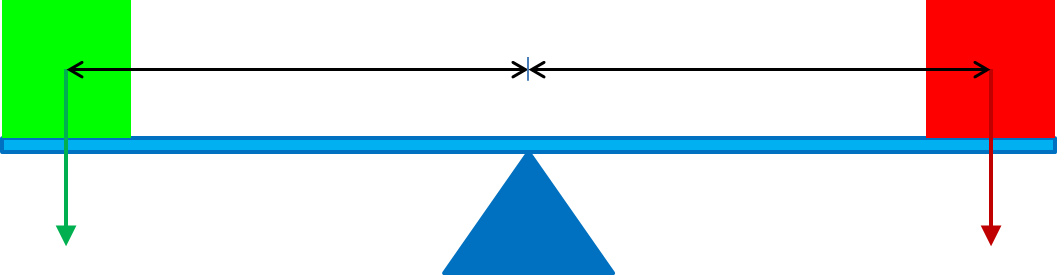
Figuur 10: De hefboomwerking is goed te demonstreren met een wip op een speelplaats.
In figuur 10 is een voorbeeld te zien waarbij de hefboomwerking van toepassing is: de wip. Een wip heeft eigenlijk twee armen die draaibaar zijn opgesteld aan beide zijden van de centraal draaipunt. Als de krachten aan beide zijden van het draaipunt in evenwicht zijn, werkt de wip het best. Op sommige dagen is op speelplaatsen te zien dat het hefboomprincipe (onbewust) wordt toegepast. Als ouderen met kinderen wippen, zit de oudere vaak niet aan het uiteinde, maar meer naar het midden toe. Door dichter bij het draaipunt plaats te nemen, wordt de kracht minder en kan de wip op enig moment ook in evenwicht zijn. De formule die hierop kan worden toegepast is:
F1 x r1 = F2 x r2
Formule 19: De formule voor de hefboomwerking.
In deze formule staat "F" voor "kracht", in Newton (N) en "r"(van het Latijnse "radius") geeft de afstand aan tot het draaipunt. De "=" kan worden gezien als de plaats van het draaipunt.
In figuur 11 zijn de onderdelen van formule 19 ingetekend, zodat duidelijk is wat ermee wordt bedoeld.
Figuur 11: De wip met de bij de formule betrokken onderdelen op hun plaats.
Als beide kanten van het "="-teken gelijk zijn, is de wip (balans) in evenwicht. In dit geval zal duidelijk zijn dat de beide krachten F 1 en F2 aan elkaar gelijk zijn. Immers, de gewichten zijn gelijk en de afstand tot het draaipunt is aan beide kanten hetzelfde. Het verandert pas als er een verschuiving van het gewicht plaats vindt. Als bijvoorbeeld F1 dichter naar het draaipunt toe gaat, raakt de wip uit evenwicht en zal de rechterkant gaan zakken. Dat kan alleen worden voorkomen door F1 groter te maken. Hoeveel groter kan uit formule 19 worden berekend. Deze formule heeft een grote gelijkenis met een eerder gebruikte formule met verhouding van oppervlakten bij druk. Dat wordt duidelijker als deze formule iets anders wordt opgeschreven, zoals hieronder in formule 20
F2 = r1 /r2 .F1
Formule 20: De uitgeoefende kracht bij een balans is te berekenen als de verhouding van de lengte van beide armen bekend is.
Ook hier is de vergroting van de kracht in verhouding met de grootte van de "armen" aan beide zijden van het draaipunt. De hefboomwerking is hiermee wel uitgelegd, maar bij een wip verandert de richting van de kracht aan de andere kant van het draaipunt. Als aan de linkerkant de wip omlaag geduwd wordt, gaat de andere kant omhoog. In het middenoor, waar ook een hefboom werkt, is dit echter niet het geval. Daar blijft de richting van de kracht gelijk. In figuur 12 wordt de beweging van de gehoorbeenketen schematisch weergegeven.
In dit figuur is goed te zien dat de hamer en het aambeeld als het ware als één geheel bewegen om een as die zich bevindt op de plaats waar beide gehoorbeentjes samenkomen. Er wordt op deze manier een systeem gemaakt waarbij de beweging van het tweede deel in dezelfde richting is als de beweging van het eerste deel. Het systeem heeft twee "armen", waarbij het eerste deel langer is dan het tweede deel. De verhouding van deze twee "armen" is 1,3 : 1.
Deze verhouding kan in formule 20 worden ingevuld om te zien hoeveel versterking deze constructie oplevert:
F2 = r1 /r2 .F1 ⇒ F2 = 1,3 / 1 .F1 ⇒ F2 = 1,3 F1
De constructie van de gehoorbeentjes levert dus een versterking op van een factor 1,3.
De totale versterking van het middenoor
Er zijn in het middenoor, zoals hierboven vermeld, twee effecten werkzaam:
- Het oppervlakte-effect, versterkingsfactor 20
- De hefboomwerking, versterkingsfactor 1,3.
Totale versterking = Oppervlakte-effect x Hefboomwerking = 20 x 1,3 = 26 keer
Deze versterkingsfactor kan worden toegepast op de geluidsdruk die het trommelvlies in beweging zet. Dus zou er ook geschreven kunnen worden:
POvale venster = 26 x PTrommelvlies
Deze berekening laat goed zien dat er een behoorlijke versterking optreedt, een factor 26. Maar hoeveel is dat in decibel? Ook dat kan uitgerekend worden. Daarvoor moet gebruik gemaakt worden van de eerder al gebruikte formule 1. Met deze formule wordt het geluidsdrukniveau van een gemeten geluidsdruk berekend in verhouding tot de geluidsdruk bij de hoordrempel van de goedhorende. Maar voor deze waarde (P0) wordt nu de geluidsdruk bij het trommelvlies genomen. Voor de gemeten geluidsdruk (P)wordt een geluidsdruk genomen die 26 keer zo groot is.
Omdat de versterking van het middenoor voor elke geluidsdruk gelijk is, hoeft er niet met een bepaalde vaste geluidsdruk gewerkt te worden. Daarom wordt voor de geluidsdruk bij het trommelvlies PTV genomen. De geluidsdruk bij het ovale venster is 26 keer zo groot, en is dus 26PTV. Ingevuld in formule 1 levert dit:
VersterkingMO = 20.log (26 x PTV/ PTV) Dit wordt: VersterkingMO = 20.log 26
Verder uitgewerkt:
VersterkingMO = 20.log 26 De logaritme van 26 nemen (rekenmachine): log 26 = 1,41
Invullen in de formule:
VersterkingMO = 20 x 1,41
Dus wordt het uiteindelijk:
VersterkingMO = 28 dB
OPGAVE 1
Door op het icoon hiernaast te klikken opent een apart scherm waarin kan worden geoefend met getallen met een exponent.